深挖题目信息，巧解电磁场中的边界问题

(2012·黄冈中学5月模考)

      如图所示，在xOy坐标系中分布三个有界场区：第一象限中有一半径为r =0.1 m的圆形磁场区域，磁感应强度B1=1T，方向垂直纸面向里，该区域同时与y轴、x轴相切，切点分别为A、C；第四象限中，由y轴、抛物线FG（y=-10x2+x-0.025，单位：m）和直线DH（y=x-0.425，单位：m）构成的区域中，存在着方向竖直向下、场强E=2.5 N/C的匀强电场；第四象限中，直线DH右下方存在垂直纸面向里的匀强磁场，磁场的磁感应强度B2=0.5 T．现有大量质量为m=1×10-16kg（不计重力和粒子间的相互作用力）、电荷量为q=2×10-14C、速率均为v=20 m/s的带负电的粒子从A处垂直磁场方向进入第一象限，速度方向与y轴所成的角在0至180°之间．

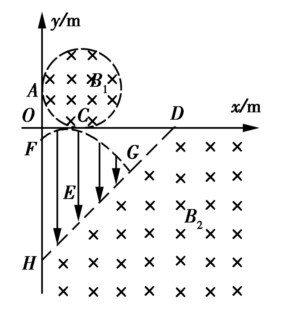
（1）求这些粒子在圆形磁场区域中运动的半径；

（2）试证明这些粒子经过x轴时的速度方向均与x轴垂直；

（3）通过计算说明这些粒子会经过y轴上的同一点，并求出该点的坐标．

【解析】 

(1)粒子在圆形磁场区域中运动时洛伦兹力等于向心力，即B1qv=mv2/ R1 ①

得R1=0.1 m.②

(2)从A点以任意方向进入磁场的粒子，设其从K点离开磁场，如图所示，O1和O2分别是磁场区域的圆心和粒子做圆周运动的圆心，因为粒子运动半径和磁场区域半径相同，因此O1AO2K为菱形，O2K平行于x轴，又因粒子离开磁场时粒子的速度垂直于O2K，即垂直于x轴，得证．

（3）设粒子在第四象限进入电场时的坐标为（x1，y1），离开电场时的坐标为（x1，y2），离开电场时速度为v2，在第四象限的磁场区域内做圆周运动的半径为R2，有

qE(y2-y1)=mv22/2 - mv2/2 ③

B2qv2=mv22/R2 ④ 

并将y1=-10x12+x1-0.025和y2=x1-0.425代入③式

联立解得R2=x1 ⑤

因v2的方向与DH成45°角，且半径刚好为x1坐标值，则这些粒子做圆周运动的圆心必在y轴上，在此磁场中恰好经过四分之一圆周，并且刚好到达同一点H处，H点坐标为（0，-0.425 m）．

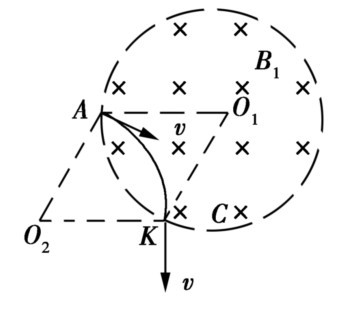
【品鉴与反思】

本题涉及带电粒子通过由抛物线FG（y=-10x2+x-0.025）和直线DH(y=x-0.425）边界决定的匀强电场区域，给考生带来全新的视觉感受，物理情境新颖，同时也使部分考生感到畏惧，认定试题难度一定很大，心理上首先就败下阵来，这是考试之大忌．

考试就像打仗，既考查考生的知识技能，又检验考生的心理素质．任何一次考试，都有可能出现新情境试题，只要我们在平时的练习中养成良好的解题习惯、认真审题、处乱不惊，必定能取得好的成绩．

(1)细读题，慢审题

审题的第一步是读题，细读慢审，特别注意括号内的内容，不可忽视．例如本题对粒子进行受力分析时，考虑到粒子质量为m=1×10-16kg,在微观粒子中这个质量不算小，因此部分考生认为粒子受到重力作用，还有部分考生认为，大量粒子间存在相互作用的库仑力，对括号内的说明视而不见，当解题不顺时，才又回头看题，这是非常不好的习惯，既耽误时间，又极易导致解答错误．

本题有三个独立场区，在圆形磁场区与电场区之间存在无场区。

一般考查带电粒子进入电场的方向有两种：垂直电场线进(出)和沿电场线进（出）电场.第(2)问证明了带电粒子穿过x轴时速度方向与x轴垂直，因此这些带电粒子一定是沿电场线方向进入电场的，由此可判断电场力做负功，粒子动能减少，由于电场区域边界的特殊性，从x轴上不同位置进入电场的粒子，电场力做功不同，粒子的动能变化量不同，所以当粒子再次进入磁场时运动的轨迹半径不同．

(2)同种带电粒子进、出圆形磁场区的规律

解题过程中要注意总结同种带电粒子进、出圆形磁场区的规律，常见的有两种：

①指向圆心进入，则背离圆心射出.

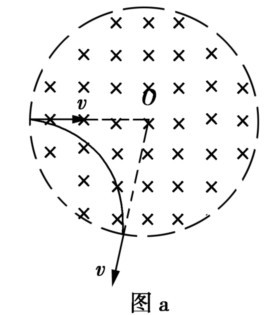
如图a，当带电粒子以指向磁场圆心方向的速度进入圆形磁场时，无论轨道半径多大，无论偏转角多大，粒子一定沿背离磁场圆心的方向从磁场中射出．

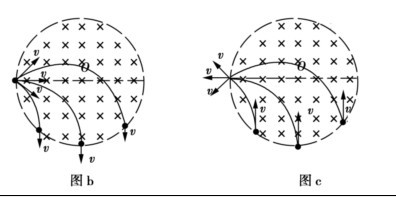
②当带电粒子轨道半径等于磁场区半径时，点入平行出或平行入点出.

如本题的第(2)问，当带电粒子在圆形磁场区运动的轨道半径等于磁场区半径时，从某点射入磁场的粒子将以相互平行的速度射出磁场（磁发散）；相反，当粒子以相互平行的速度进入磁场，偏转后将从同一点射出磁场（磁聚焦），且过该点的圆形磁场的半径与粒子射入时的平行速度方向垂直.如图b、c．

(3)充分利用数学关系解题

    在看似复杂的边界问题中，只要代入表示边界的方程，即可确定射入和射出点的坐标，同时注意坐标点间的几何关系，定能突破试题难点．

     第(3)问，由于带电粒子沿电场线运动，进、出电场时的x1坐标相同，因此只需将进入电场时的抛物线方程和出电场时的直线方程代入③式，联立④式即可得到R2=x1的简单关系，试题看似复杂，结果却非常简单．

     电磁学中更多精彩内容，如：“磁偏转”和“电偏转”模型的区别、带电粒子在复合场中的运动状态的分析、如何解决带电粒子在磁场中运动的多解和临界问题、导体棒在磁场中运动的收尾速度问题常见模型透析、交流电路的动态问题的分析方法等。